Relasi Sudut Trigonometri

Relasi Sudut

1. Kuadran

Rendered by QuickLaTeX.com

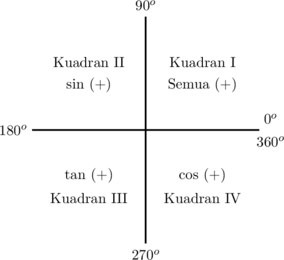
2. Sudut Istimewa di kuadran I ( $0^{o} < α < 90^{o}$ )

	0°	30°	45°	60°	90°
Sin	0	$\frac{1}{2}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2} \sqrt{3}$	1
Cos	1	$\frac{1}{2} \sqrt{3}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2}$	0
Tan	0	$\frac{1}{3} \sqrt{3}$	1	$\sqrt{3}$	∼

3. Sudut di kuadran II ( $90^{o} < α < 180^{o}$ )

Menggunakan $(180^{o} - α)$	Menggunakan $(90^{o} + α)$
$\begin{aligned} \sin 150^{o} & = \sin (180^{o} - 30^{o}) \\ \sin 150^{o} & = + \sin 30^{o} \\ \sin 150^{o} & = + \frac{1}{2} \end{aligned}$ 150º berada di kuadran II, maka sin 150º bernilai positif.	$\begin{aligned} \sin 150^{o} & = \sin (90^{o} + 60^{o}) \\ \sin 150^{o} & = + \cos 60^{o} \sin \to \cos \\ \sin 150^{o} & = + \frac{1}{2} \end{aligned}$ 150º berada di kuadran II, maka sin 150º bernilai positif.
$\begin{aligned} \cos 150^{o} & = \cos (180^{o} - 30^{o}) \\ \cos 150^{o} & = - \cos 30^{o} \\ \cos 150^{o} & = - \frac{1}{2} \sqrt{3} \end{aligned}$ 150º berada di kuadran II, maka cos 150º bernilai negatif.	$\begin{aligned} \cos 150^{o} & = \cos (90^{o} + 60^{o}) \\ \cos 150^{o} & = - \sin 60^{o} \cos \to \sin \\ \cos 150^{o} & = - \frac{1}{2} \sqrt{3} \end{aligned}$ 150º berada di kuadran II, maka cos 150º bernilai negatif.
$\begin{aligned} \tan 150^{o} & = \tan (180^{o} - 30^{o}) \\ \tan 150^{o} & = - \tan 30^{o} \\ \tan 150^{o} & = - \frac{1}{3} \sqrt{3} \end{aligned}$ 150º berada di kuadran II, maka tan 150º bernilai negatif.	$\begin{aligned} \tan 150^{o} & = \tan (90^{o} + 60^{o}) \\ \tan 150^{o} & = - \cot 60^{o} \tan \to \cot \\ \tan 150^{o} & = - \frac{1}{3} \sqrt{3} \end{aligned}$ 150º berada di kuadran II, maka tan 150º bernilai negatif.
$\begin{aligned} \sin 180^{o} & = \sin (180^{o} - 0^{o}) \\ \sin 180^{o} & = \sin 0^{o} \\ \sin 180^{o} & = 0 \end{aligned}$	$\begin{aligned} \sin 180^{o} & = \sin (90^{o} + 90^{o}) \\ \sin 180^{o} & = \cos 90^{o} \sin \to \cos \\ \sin 180^{o} & = 0 \end{aligned}$

Menggunakan

(180^{o} - α)

Menggunakan

(90^{o} + α)

$\begin{aligned} \sin 150^{o} & = \sin (180^{o} - 30^{o}) \\ \sin 150^{o} & = + \sin 30^{o} \\ \sin 150^{o} & = + \frac{1}{2} \end{aligned}$

150º berada di kuadran II, maka sin 150º bernilai positif.

$\begin{aligned} \sin 150^{o} & = \sin (90^{o} + 60^{o}) \\ \sin 150^{o} & = + \cos 60^{o} \sin \to \cos \\ \sin 150^{o} & = + \frac{1}{2} \end{aligned}$

150º berada di kuadran II, maka sin 150º bernilai positif.

$\begin{aligned} \cos 150^{o} & = \cos (180^{o} - 30^{o}) \\ \cos 150^{o} & = - \cos 30^{o} \\ \cos 150^{o} & = - \frac{1}{2} \sqrt{3} \end{aligned}$

150º berada di kuadran II, maka cos 150º bernilai negatif.

$\begin{aligned} \cos 150^{o} & = \cos (90^{o} + 60^{o}) \\ \cos 150^{o} & = - \sin 60^{o} \cos \to \sin \\ \cos 150^{o} & = - \frac{1}{2} \sqrt{3} \end{aligned}$

150º berada di kuadran II, maka cos 150º bernilai negatif.

$\begin{aligned} \tan 150^{o} & = \tan (180^{o} - 30^{o}) \\ \tan 150^{o} & = - \tan 30^{o} \\ \tan 150^{o} & = - \frac{1}{3} \sqrt{3} \end{aligned}$

150º berada di kuadran II, maka tan 150º bernilai negatif.

$\begin{aligned} \tan 150^{o} & = \tan (90^{o} + 60^{o}) \\ \tan 150^{o} & = - \cot 60^{o} \tan \to \cot \\ \tan 150^{o} & = - \frac{1}{3} \sqrt{3} \end{aligned}$

150º berada di kuadran II, maka tan 150º bernilai negatif.

$\begin{aligned} \sin 180^{o} & = \sin (180^{o} - 0^{o}) \\ \sin 180^{o} & = \sin 0^{o} \\ \sin 180^{o} & = 0 \end{aligned}$

\begin{aligned} \sin 180^{o} & = \sin (90^{o} + 90^{o}) \\ \sin 180^{o} & = \cos 90^{o} \sin \to \cos \\ \sin 180^{o} & = 0 \end{aligned}

4. Sudut di kuadran III ( $180^{o} < α < 270^{o}$ )

Menggunakan $(180^{o} + α)$	Menggunakan $(270^{o} - α)$
$\begin{aligned} \sin 225^{o} & = \sin (180^{o} + 45^{o}) \\ \sin 225^{o} & = - \sin 45^{o} \\ \sin 225^{o} & = - \frac{1}{2} \sqrt{2} \end{aligned}$ 225º berada di kuadran III, maka sin 225º bernilai negatif.	$\begin{aligned} \sin 225^{o} & = \sin (270^{o} - 45^{o}) \\ \sin 225^{o} & = - \cos 45^{o} \sin \to \cos \\ \sin 225^{o} & = - \frac{1}{2} \sqrt{2} \end{aligned}$ 225º berada di kuadran III, maka sin 225º bernilai negatif.
$\begin{aligned} \cos 225^{o} & = \cos (180^{o} + 45^{o}) \\ \cos 225^{o} & = - \cos 45^{o} \\ \cos 225^{o} & = - \frac{1}{2} \sqrt{2} \end{aligned}$ 225º berada di kuadran III, maka cos 225º bernilai negatif.	$\begin{aligned} \cos 225^{o} & = \cos (270^{o} - 45^{o}) \\ \cos 225^{o} & = - \sin 45^{o} \cos \to \sin \\ \cos 225^{o} & = - \frac{1}{2} \sqrt{2} \end{aligned}$ 225º berada di kuadran III, maka cos 225º bernilai negatif.
$\begin{aligned} \tan 225^{o} & = \tan (180^{o} + 45^{o}) \\ \tan 225^{o} & = + \tan 45^{o} \\ \tan 225^{o} & = + 1 \end{aligned}$ 225º berada di kuadran III, maka tan 225º bernilai positif.	$\begin{aligned} \tan 225^{o} & = \tan (270^{o} - 45^{o}) \\ \tan 225^{o} & = + \cot 45^{o} \tan \to \cot \\ \tan 225^{o} & = + 1 \end{aligned}$ 225º berada di kuadran III, maka tan 225º bernilai positif.
$\begin{aligned} \sin 270^{o} & = \sin (180^{o} + 90^{o}) \\ \sin 270^{o} & = - \sin 90^{o} \\ \sin 270^{o} & = - 1 \end{aligned}$ 270º berada di kuadran III atau IV, maka sin 270º bernilai negatif.	$\begin{aligned} \sin 270^{o} & = \sin (270^{o} - 0^{o}) \\ \sin 270^{o} & = - \cos 0^{o} \\ \sin 270^{o} & = - 1 \end{aligned}$ 270º berada di kuadran III atau IV, maka sin 270º bernilai negatif.

Menggunakan

(180^{o} + α)

Menggunakan

(270^{o} - α)

$\begin{aligned} \sin 225^{o} & = \sin (180^{o} + 45^{o}) \\ \sin 225^{o} & = - \sin 45^{o} \\ \sin 225^{o} & = - \frac{1}{2} \sqrt{2} \end{aligned}$

225º berada di kuadran III, maka sin 225º bernilai negatif.

$\begin{aligned} \sin 225^{o} & = \sin (270^{o} - 45^{o}) \\ \sin 225^{o} & = - \cos 45^{o} \sin \to \cos \\ \sin 225^{o} & = - \frac{1}{2} \sqrt{2} \end{aligned}$

225º berada di kuadran III, maka sin 225º bernilai negatif.

$\begin{aligned} \cos 225^{o} & = \cos (180^{o} + 45^{o}) \\ \cos 225^{o} & = - \cos 45^{o} \\ \cos 225^{o} & = - \frac{1}{2} \sqrt{2} \end{aligned}$

225º berada di kuadran III, maka cos 225º bernilai negatif.

$\begin{aligned} \cos 225^{o} & = \cos (270^{o} - 45^{o}) \\ \cos 225^{o} & = - \sin 45^{o} \cos \to \sin \\ \cos 225^{o} & = - \frac{1}{2} \sqrt{2} \end{aligned}$

225º berada di kuadran III, maka cos 225º bernilai negatif.

$\begin{aligned} \tan 225^{o} & = \tan (180^{o} + 45^{o}) \\ \tan 225^{o} & = + \tan 45^{o} \\ \tan 225^{o} & = + 1 \end{aligned}$

225º berada di kuadran III, maka tan 225º bernilai positif.

$\begin{aligned} \tan 225^{o} & = \tan (270^{o} - 45^{o}) \\ \tan 225^{o} & = + \cot 45^{o} \tan \to \cot \\ \tan 225^{o} & = + 1 \end{aligned}$

225º berada di kuadran III, maka tan 225º bernilai positif.

$\begin{aligned} \sin 270^{o} & = \sin (180^{o} + 90^{o}) \\ \sin 270^{o} & = - \sin 90^{o} \\ \sin 270^{o} & = - 1 \end{aligned}$

270º berada di kuadran III atau IV, maka sin 270º bernilai negatif.

\begin{aligned} \sin 270^{o} & = \sin (270^{o} - 0^{o}) \\ \sin 270^{o} & = - \cos 0^{o} \\ \sin 270^{o} & = - 1 \end{aligned}

270º berada di kuadran III atau IV, maka sin 270º bernilai negatif.

5. Sudut di kuadran IV ( $270^{o} < α < 360^{o}$ )

Menggunakan $(360^{o} - α)$	Menggunakan $(270^{o} + α)$
$\begin{aligned} \sin 300^{o} & = \sin (360^{o} - 60^{o}) \\ \sin 300^{o} & = - \sin 60^{o} \\ \sin 300^{o} & = - \frac{1}{2} \sqrt{3} \end{aligned}$ 300º berada di kuadran IV, maka sin 300º bernilai negatif.	$\begin{aligned} \sin 300^{o} & = \sin (270^{o} + 30^{o}) \\ \sin 300^{o} & = - \cos 30^{o} \sin \to \cos \\ \sin 300^{o} & = - \frac{1}{2} \sqrt{3} \end{aligned}$ 300º berada di kuadran II, maka sin 300º bernilai positif.
$\begin{aligned} \cos 300^{o} & = \cos (360^{o} - 60^{o}) \\ \cos 300^{o} & = + \cos 60^{o} \\ \cos 300^{o} & = + \frac{1}{2} \end{aligned}$ 300º berada di kuadran IV, maka cos 300º bernilai positif.	$\begin{aligned} \cos 300^{o} & = \cos (270^{o} + 30^{o}) \\ \cos 300^{o} & = + \sin 30^{o} \cos \to \sin \\ \cos 300^{o} & = + \frac{1}{2} \end{aligned}$ 300º berada di kuadran II, maka cos 300º bernilai negatif.
$\begin{aligned} \tan 300^{o} & = \tan (360^{o} - 60^{o}) \\ \tan 300^{o} & = - \tan 60^{o} \\ \tan 300^{o} & = - \sqrt{3} \end{aligned}$ 300º berada di kuadran IV, maka tan 300º bernilai negatif.	$\begin{aligned} \tan 300^{o} & = \tan (270^{o} + 30^{o}) \\ \tan 300^{o} & = - \cot 30^{o} \tan \to \cot \\ \tan 300^{o} & = - \sqrt{3} \end{aligned}$ 300º berada di kuadran II, maka tan 300º bernilai negatif.

Menggunakan

(360^{o} - α)

Menggunakan

(270^{o} + α)

$\begin{aligned} \sin 300^{o} & = \sin (360^{o} - 60^{o}) \\ \sin 300^{o} & = - \sin 60^{o} \\ \sin 300^{o} & = - \frac{1}{2} \sqrt{3} \end{aligned}$

300º berada di kuadran IV, maka sin 300º bernilai negatif.

$\begin{aligned} \sin 300^{o} & = \sin (270^{o} + 30^{o}) \\ \sin 300^{o} & = - \cos 30^{o} \sin \to \cos \\ \sin 300^{o} & = - \frac{1}{2} \sqrt{3} \end{aligned}$

300º berada di kuadran II, maka sin 300º bernilai positif.

$\begin{aligned} \cos 300^{o} & = \cos (360^{o} - 60^{o}) \\ \cos 300^{o} & = + \cos 60^{o} \\ \cos 300^{o} & = + \frac{1}{2} \end{aligned}$

300º berada di kuadran IV, maka cos 300º bernilai positif.

$\begin{aligned} \cos 300^{o} & = \cos (270^{o} + 30^{o}) \\ \cos 300^{o} & = + \sin 30^{o} \cos \to \sin \\ \cos 300^{o} & = + \frac{1}{2} \end{aligned}$

300º berada di kuadran II, maka cos 300º bernilai negatif.

$\begin{aligned} \tan 300^{o} & = \tan (360^{o} - 60^{o}) \\ \tan 300^{o} & = - \tan 60^{o} \\ \tan 300^{o} & = - \sqrt{3} \end{aligned}$

300º berada di kuadran IV, maka tan 300º bernilai negatif.

$\begin{aligned} \tan 300^{o} & = \tan (270^{o} + 30^{o}) \\ \tan 300^{o} & = - \cot 30^{o} \tan \to \cot \\ \tan 300^{o} & = - \sqrt{3} \end{aligned}$

300º berada di kuadran II, maka tan 300º bernilai negatif.

Sudut-sudut Besar

Untuk sudut-sudut yang lebih besar dari 360°, yang dihitung adalah sisa sudut setelah dikurangi kelipatan 360°.

Contoh 01

$\begin{aligned} \sin 1470^{o} & = \sin (360^{o} . 4 + 30^{o}) \\ \sin 1470^{o} & = \sin 30^{o} \\ \sin 1470^{o} & = \frac{1}{2} \end{aligned}$

Contoh 02

$\begin{aligned} \tan 855^{o} & = \tan (360^{o} . 2 + 135^{o}) \\ \tan 855^{o} & = \tan 135^{o} \\ \tan 855^{o} & = \tan (180^{o} - 45^{o}) \\ \tan 855^{o} & = - \tan 45^{o} \\ \tan 855^{o} & = - 1 \end{aligned}$

Sudut-sudut Negatif

Sudut negatif diasumsikan pada kuadran 4.

$\sin (- α) = - \sin α$

Sinus sudut pada kuadran 4 bernilai negatif.

$\cos (- α) = \cos α$

Cosinus sudut pada kuadran 4 bernilai positif.

$\tan (- α) = - \tan α$

Tangen sudut pada kuadran 4 bernilai negatif.

Contoh 01

$\begin{aligned} \sin (- 240^{o}) & = - \sin 240^{o} \\ \sin (- 240^{o}) & = - \sin (180^{o} + 60^{o}) \\ \sin (- 240^{o}) & = - (- \sin 60^{o}) \\ \sin (- 240^{o}) & = \sin 60^{o} \\ \sin (- 240^{o}) & = \frac{1}{2} \sqrt{3} \end{aligned}$

Contoh 02

$\begin{aligned} \cos (- 135^{o}) & = + \cos 135^{o} \\ \cos (- 135^{o}) & = \cos (180^{o} - 45^{o}) \\ \cos (- 135^{o}) & = - \cos 45^{o} \\ \cos (- 135^{o}) & = - \frac{1}{2} \sqrt{2} \end{aligned}$

Sudut-sudut Sembarang

Sudut-sudut yang bukan sudut istimewa dicari hubungannya dengan menggunakan relasi sudut.

Contoh 01

Tentukan nilai eksak dari $\frac{\sin 20^{o}}{\cos 110^{o}}$

$\begin{aligned} \frac{\sin 20^{o}}{\cos 110^{o}} \\ \frac{\sin 20^{o}}{\cos (90^{o} + 20^{o})} \\ \frac{\sin 20^{o}}{- \sin 20^{o}} \\ - 1 \end{aligned}$

Contoh 02

Tentukan nilai eksak dari $\tan 156^{o} . \frac{\cos 336^{o}}{\sin 204^{o}}$

$\begin{aligned} \tan 156^{o} . \frac{\cos 336^{o}}{\sin 204^{o}} \\ \frac{\sin 156^{o}}{\cos 156^{o}} . \frac{\cos 336^{o}}{\sin 204^{o}} \\ \frac{\sin (180^{o} - 24^{o})}{\cos (180^{o} - 24^{o})} . \frac{\cos (360^{o} - 24^{o})}{\sin (180^{o} + 24^{o})} \\ \frac{\sin 24^{o}}{- \cos 24^{o}} . \frac{\cos 24^{o}}{- \sin 24^{o}} \\ 1 \end{aligned}$

SOAL LATIHAN

--- Buka halaman ini ---

Relasi Sudut

Sudut-sudut Besar

Sudut-sudut Negatif

Sudut-sudut Sembarang

SOAL LATIHAN

Perbandingan Trigonometri