Segitiga Siku-siku
1. Segitiga Siku-siku
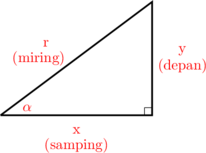
\(\sin \alpha = \dfrac yr = \dfrac {\text{depan}}{\text{miring}}\)
\(\cos \alpha = \dfrac xr = \dfrac {\text{samping}}{\text{miring}}\)
\(\tan \alpha = \dfrac yx = \dfrac {\text{depan}}{\text{samping}}\)
\(\sec \alpha = \dfrac {1}{\cos \alpha} \)
\(\csc \alpha = \dfrac {1}{\sin \alpha} \)
\(\cot \alpha = \dfrac {1}{\tan \alpha} \)
2. Sudut Istimewa
| \(0\) | \(30^{\text{o}}\) | \(45^{\text{o}}\) | \(60^{\text{o}}\) | \(90^{\text{o}}\) | \(37^{\text{o}}\) | \(53^{\text{o}}\) | |
|---|---|---|---|---|---|---|---|
| Sin | 0 | \(\dfrac{1}{2}\) | \(\dfrac{1}{2}\sqrt{2}\) | \(\dfrac{1}{2}\sqrt{3}\) | 1 | \(0,6\) | \(0,8\) |
| Cos | 1 | \(\dfrac{1}{2}\sqrt{3}\) | \(\dfrac{1}{2}\sqrt{2}\) | \(\dfrac{1}{2}\) | 0 | \(0,8\) | \(0,6\) |
| Tan | 0 | \(\dfrac{1}{3} \sqrt{3}\) | 1 | \(\sqrt{3}\) | ∼ | \(\dfrac 34\) | \(\dfrac 43\) |
Contoh 01
Diketahui segitiga siku-siku di bawah ini:
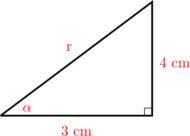
Tentukan nilai dari \(\sin \alpha\), \(\cos \alpha\) dan \(\tan \alpha\)
Menentukan nilai r
\begin{equation*} \begin{split} x^2 + 5^2 & = r^2 \\\\ 3^2 + 4^2 & = r^2 \\\\ 9 + 16 & = r^2 \\\\ 25 & = r^2 \\\\ r & = \pm 5 \end{split} \end{equation*}
Gunakan nilai positif untuk \(r = 5\)
\begin{equation*} \sin \alpha = \frac {\text{depan}}{\text{miring}} = \bbox[5px, border: 2px solid magenta] {\frac {4}{5}} \end{equation*}
\begin{equation*} \cos \alpha = \frac {\text{samping}}{\text{miring}} = \bbox[5px, border: 2px solid magenta] {\frac {3}{5}} \end{equation*}
\begin{equation*} \tan \alpha = \frac {\text{depan}}{\text{samping}} = \bbox[5px, border: 2px solid magenta] {\frac {4}{3}} \end{equation*}
Contoh 02
Pada sebuah segitiga siku-siku ABC, diketahui nilai dari \(\sin A = \dfrac {5}{13}\).
Tentukan nilai dari \(\cos A\) dan \(\tan A\)
\(\sin A = \dfrac yr = \dfrac {\text{depan}}{\text{miring}} = \dfrac {5}{13}\)

Menentukan nilai \(x\)
\begin{equation*} \begin{split} x^2 + 5^2 & = 13^2 \\\\ x^2 + 25 & = 169 \\\\ x^2 & = 144 \\\\ x & = \pm 12 \end{split} \end{equation*}
Karena panjang AB harus bernilai positif, maka \(x = 12\)
\(\cos A = \dfrac xr = \dfrac {\text{samping}}{\text{miring}} = \bbox[5px, border: 2px solid magenta] {\dfrac {12}{13}}\)
\(\tan A = \dfrac yx = \dfrac {\text{depan}}{\text{samping}} = \bbox[5px, border: 2px solid magenta] {\dfrac {5}{12}}\)
SOAL LATIHAN
