Alat Ukur Kecepatan Fluida
A. Venturimeter terbuka
Venturimeter terbuka digunakan untuk mengukur kelajuan aliran zat cair.

\(A_1 > A_2 \rightarrow v_1 < v_2 \rightarrow P_1 > P_2\)
Permukaan cairan pada pipa (1) lebih tinggi daripada permukaan cairan pada pipa (2)
Penurunan Rumus
\(P_1 + \rho \: g \: h_1 + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \rho \: g \: h_2 + \frac{1}{2} \: \rho \: v_2^2\)
Titik (1) dan (2) sejajar, maka \(h_1 = h_2\)
\(P_1 + \cancel {\rho \: g \: h_1} + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \cancel {\rho \: g \: h_2} + \frac{1}{2} \: \rho \: v_2^2\)
\(P_1 + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \frac{1}{2} \: \rho \: v_2^2\)
\(P_1 - P_2 = \frac{1}{2} \: \rho \: v_2^2 - \frac{1}{2} \: \rho \: v_1^2\)
\(\Delta P = \frac{1}{2} \: \rho \: (v_2^2 - v_1^2)\)
Tekanan pada pipa adalah tekanan hidrostatis \(P = \rho \: g \: h\)
\(\rho \: g \: \Delta h = \frac{1}{2} \: \rho \: (v_2^2 - v_1^2)\)
\(\cancel {\rho} \: g \: \Delta h = \frac{1}{2} \: \cancel {\rho} \: (v_2^2 - v_1^2)\)
\(2 \: g \: \Delta h = (v_2^2 - v_1^2)\)
Persamaan kontinuitas \(A_1 \: v_1 = A_2 \: v_2 \rightarrow v_2 = \dfrac {A_1}{A_2} \: v_1\)
\(2 \: g \: \Delta h = \left[\left(\dfrac {A_1}{A_2} \:.\: v_1\right)^2 - v_1^2\right]\)
\(2 \: g \: \Delta h = \left[\left(\dfrac {A_1}{A_2}\right)^2 - 1\right] \:.\: v_1^2\)
\(v_1^2 = \dfrac{2 \: g \: \Delta h}{\left[\left(\dfrac {A_1}{A_2}\right)^2 - 1\right]}\)
\(v_1 = \sqrt {\dfrac{2 \: g \: \Delta h}{\left[\left(\dfrac {A_1}{A_2}\right)^2 - 1\right]}}\)
B. Venturimeter tertutup
Venturimeter tertutup digunakan untuk mengukur kelajuan aliran air.
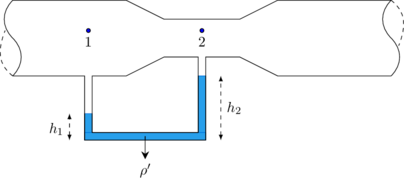
\(A_1 > A_2 \rightarrow v_1 < v_2 \rightarrow P_1 > P_2\)
Maka permukaan fluida pada pipa (1) lebih rendah daripada permukaan fluida pada pipa (2)
Penurunan Rumus
\(P_1 + \rho \: g \: h_1 + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \rho \: g \: h_2 + \frac{1}{2} \: \rho \: v_2^2\)
Titik (1) dan (2) sejajar, maka \(h_1 = h_2\)
\(P_1 + \cancel {\rho \: g \: h_1} + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \cancel {\rho \: g \: h_2} + \frac{1}{2} \: \rho \: v_2^2\)
\(P_1 + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \frac{1}{2} \: \rho \: v_2^2\)
\(P_1 - P_2 = \frac{1}{2} \: \rho \: v_2^2 - \frac{1}{2} \: \rho \: v_1^2\)
\(\rho \: g \: (-\Delta h) - \rho' \: g \: (-\Delta h) = \frac{1}{2} \: \rho \: (v_2^2 - v_1^2)\)
\(g \: \Delta h \: (\rho' - \rho) = \frac{1}{2} \: \rho \: (v_2^2 - v_1^2)\)
\(\dfrac {2 \: g \: \Delta h \: (\rho' - \rho)}{\rho} = (v_2^2 - v_1^2)\)
Persamaan kontinuitas \(A_1 \: v_1 = A_2 \: v_2 \rightarrow v_2 = \dfrac {A_1}{A_2} \: v_1\)
\(\dfrac {2 \: g \: \Delta h \: (\rho' - \rho)}{\rho} = \left[\left(\dfrac {A_1}{A_2} \:.\: v_1\right)^2 - v_1^2\right]\)
\(\dfrac {2 \: g \: \Delta h \: (\rho' - \rho)}{\rho} = \left[\left(\dfrac {A_1}{A_2}\right)^2 - 1\right] \:.\: v_1^2\)
\(v_1^2 = \dfrac{2 \: g \: \Delta h \: (\rho' - \rho)}{\rho \: \left[\left(\dfrac {A_1}{A_2}\right)^2 - 1\right]}\)
\(v_1 = \sqrt {\dfrac{2 \: g \: \Delta h \: (\rho' - \rho)}{\rho \: \left[\left(\dfrac {A_1}{A_2}\right)^2 - 1\right]}}\)
C. Tabung Pitot
tabung pitot digunakan untuk mengukur kelajuan aliran gas
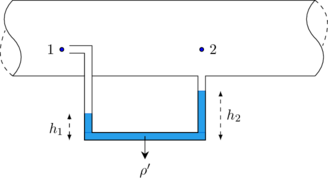
Pada tabung pitot, mulut pipa (1) diarahkan tegak lurus terhadap arah aliran gas (menjauhi pembaca), sehingga \(v_1 = 0\)
Penurunan Rumus
\(P_1 + \rho \: g \: h_1 + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \rho \: g \: h_2 + \frac{1}{2} \: \rho \: v_2^2\)
Titik (1) dan (2) sejajar, maka \(h_1 = h_2\) dan \(v_1 = 0\)
\(P_1 + \cancel {\rho \: g \: h_1} + 0 = P_2 + \cancel {\rho \: g \: h_2} + \frac{1}{2} \: \rho \: v_2^2\)
\(P_1 - P_2 = P_2 + \frac{1}{2} \: \rho \: v_2^2\)
\(\Delta P = \frac{1}{2} \: \rho \: v_2^2\)
\(\rho' \: g \: \Delta h = \frac{1}{2} \: \rho \: v_2^2\)
\(v_2^2 = \dfrac{2 \rho' \: g \: \Delta h}{\rho}\)
\(v_1 = \sqrt {\dfrac{2 \rho' \: g \: \Delta h}{\rho}}\)
SOAL LATIHAN
