Transformation of Graphs
Graph of \(y = \left| f(x) \right| \)
\(y = \begin{cases} f(x), \quad f(x) \geq 0 \\[2ex] - f(x), \quad f(x) < 0 \end{cases} \)
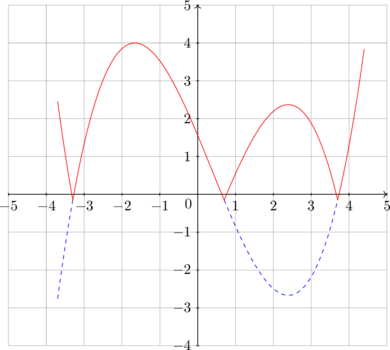
Graph of \(y = | f(x) | \) based on given \(y = f(x)\):
- part of the graph above x-axis does not change
- part of the graph below x-axis reflected about the x-axis
\(y = f(x)\)
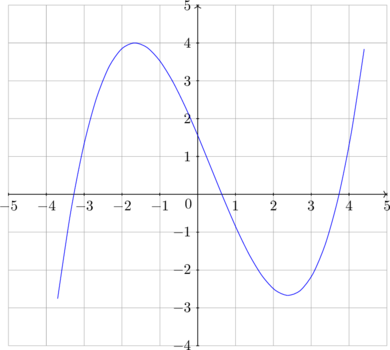
\(y = | f(x) | \)
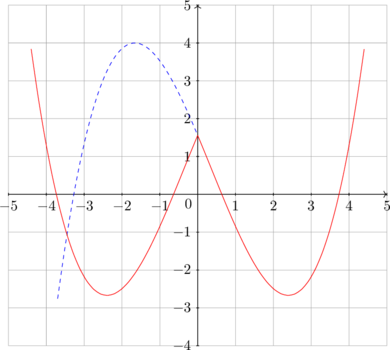
Graph of \(y = f(|x|) \)
\(f(|x|) = \begin{cases} f(x), \quad x \geq 0 \\[2ex] f(-x), \quad x < 0 \end{cases} \)

Graph of \(y = \dfrac {1}{f(x)} \)
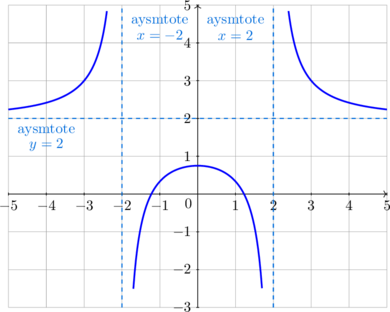
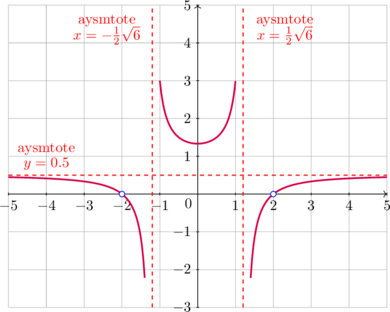
| \(y = f(x)\) | \(y = \dfrac {1}{f(x)}\) |
| For \(f(x) = 0\)
is that the x-intercept |
\(y = \dfrac {1}{f(x)}\) does not exist
x-intercept of \(y = f(x)\) becomes the vertical asymtotes |
| Vertical asymtotes of \(f(x)\) | Vertical asymtotes of \(y = f(x)\) becomes x-intercept,
but does not touch x-axis (indicate by hollow circles) |
| Maximum point at \((x,f(x))\) | Maximum point of \(y = f(x)\) becomes minimum point at \(\left(x,\dfrac {1}{f(x)}\right)\) |
| Minimum point at \((x,f(x))\) | Minimum point of \(y = f(x)\) becomes maximum point at \(\left(x,\dfrac {1}{f(x)}\right)\) |
| When \(f(x) = 1\) | \(\dfrac {1}{f(x)} = 1\)
common point |
| When \(f(x) = -1\) | \(\dfrac {1}{f(x)} = -1\)
common point |
| When \(f(x) > 0\) | \(\dfrac {1}{f(x)} > 0\) |
| When \(f(x) < 0\) | \(\dfrac {1}{f(x)} < 0\) |
| When \(f(x)\) increases | \(\dfrac {1}{f(x)}\) decreases |
| When \(f(x)\) decreases | \(\dfrac {1}{f(x)}\) increases |
Graph of \(y^2 = f(x)\)
Graph of \(y^2 = f(x)\) based on given \(y = f(x)\):
- \(y^2 = f(x) \rightarrow y = \pm \sqrt{f(x)}\)
- sketch the graph of \(y = \sqrt{f(x)}\) based on \(y = f(x)\)
- sketch the graph of \(y = -\sqrt{f(x)}\) as a reflection of \(y = \sqrt{f(x)}\)
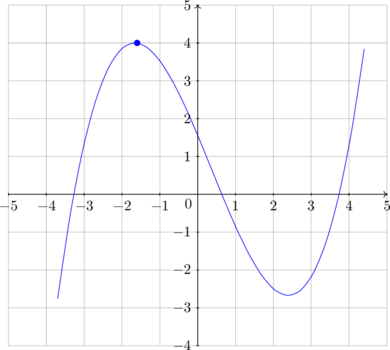
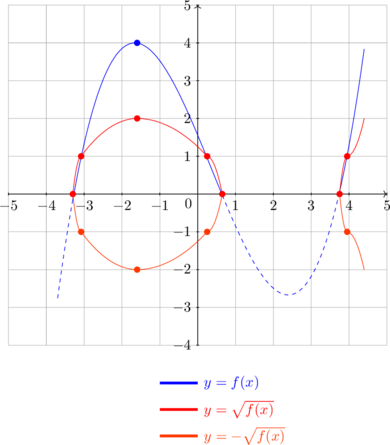
| \(y = f(x)\) | \(y = \sqrt{f(x)}\) |
| For \(f(x) < 0\) | \(\sqrt{f(x)}\) is not defined, no graph |
| For any point \((h, k)\) where \(k > 0\) | The point will become \((h, \sqrt{k})\) |
| Horizontal asymptote \(y = c\) | Horizontal asymtote will become \(y = \sqrt{c}\) |
| Vertical asymptote \(x = a\) | Vertical asymptote \(x = a\), no change |
| When \(f(x) = 0\) | \(\sqrt{f(x)} = 0\) |
| When \(f(x) = 1\) | \(\sqrt{f(x)} = 1\) |
| When \(0 < f(x) < 1\) | \(\sqrt{f(x)} > f(x)\), that means the graph will be higher |
| When \(f(x) > 1\) | \(\sqrt{f(x)} < f(x)\), that means the graph will be lower |
Exercise
