Graphs of Rational Functions
Graph of \(y = \dfrac 1x\)
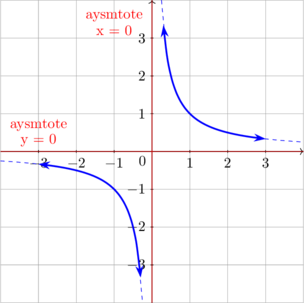
Asymtotes
For \(x \rightarrow \: \sim, \: y \rightarrow 0\)
Asymtote \(y = 0\)
For \(y \rightarrow \: \sim, \: x \rightarrow 0\)
Asymtote \(x = 0\)
The curve does not cut x-axis and y-axis
Graph of \(y = \dfrac {ax + b}{px + q}\)
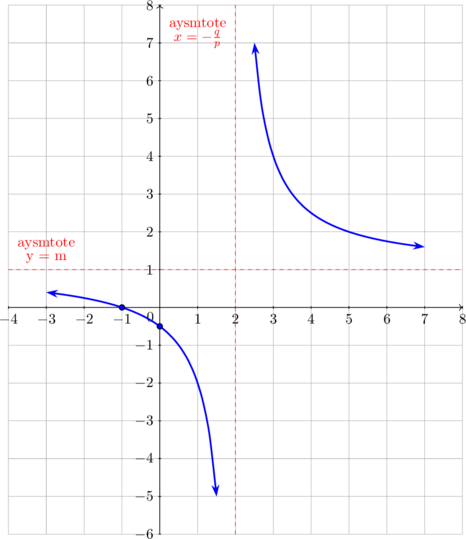
Change the form of \(y = \dfrac {ax + b}{px + q}\) into \(y = m + \dfrac {t}{px + q}\)
Asymtotes
For \(x \rightarrow \: \sim, \: y \rightarrow m\)
Horizontal asymtote \(y = m\)
For \(y \rightarrow \: \sim, \: px + q \rightarrow 0\)
Vertical asymtote \(x = - \dfrac qp\)
Axis intercept
X-intercept when y = 0
Y-intercept when x = 0
Graph of \(y = \dfrac {ax^2 + bx + c}{px + q}\)
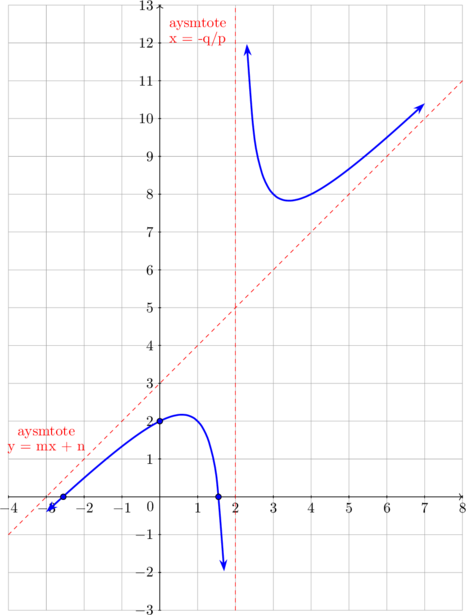
Change the form of \(y = \dfrac {ax^2 + bx + c}{px + q}\) into \(y = mx + n + \dfrac {t}{px + q}\)
Asymtotes
For \(x \rightarrow \: \sim, \: y \rightarrow mx + n\)
Oblique asymtote \(y = mx + n\)
For \(y \rightarrow \: \sim, \: px + q \rightarrow 0\)
Vertical asymtote \(x = - \dfrac qp\)
Axis intercept
X-intercept when y = 0
Y-intercept when x = 0
Exercise

