Quadratic function can be written as:
- \(f : x \rightarrow ax^2 + bx + c\)
- \(f(x) = ax^2 + bx + c\)
- \(y = ax^2 + bx + c\)
Quadratic function can be drawn in Cartesian diagram as a parabolic like below:
Concave-up parabolic curve
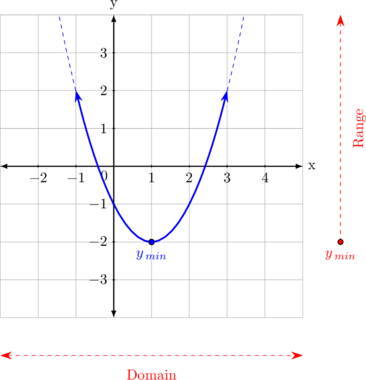
The parabolic curve can be extended to the top left and the top right, hence the value of x can be any number.
The curve has minimum value of y, but it does not have maximum value (the curve can go up to infinite), hence the value of y must be greater or equal than \(y_{min}\).
Concave-down parabolic curve
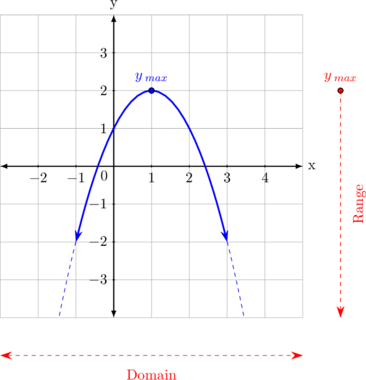
The parabolic curve can be extended to the bottom left and the bottom right, hence the value of y can be any number.
The curve has maximum value of y, but it does not have minimum value (the curve can go down to infinite), hence the value of y must be less or equal than \(y_{max}\).
Domain and Range of Quadratic Function
Domain
\(x \in R\) or can be written as \(- \sim \: < x < +\sim\)
Range for concave-up parabolic curve
\(y \geq y_{min}\)
or can be written as
\(y_{min} \leq y < + \sim\)
Range for concave-down parabolic curve
\(y \leq y_{max}\)
or can be written as
\(- \sim \: < y \leq y_{max}\)
Determine the maximum or minimum value of y of the function \(y = ax^2 + bx + c\)
First, find the x value for maximum/minimum point, \(x_{min} = - \dfrac ba\)
Then substitute the value of \(x_{min}\) into \(y = ax^2 + bx + c\) to find the value of y.

