Domain dan Range Alami
| A. Fungsi Linear | |
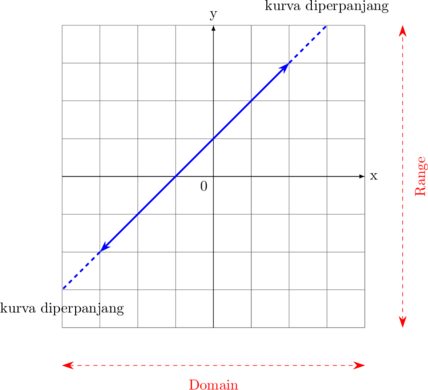
| \(y = mx + c\)
|
Domain
\(- \sim \: < x < \: \sim\)
Range \(- \sim \: < y < \: \sim\) |
|
B. Fungsi Kuadrat |
|
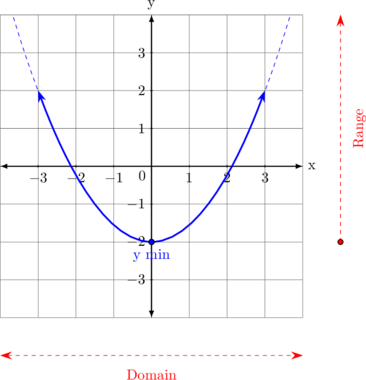
| Kurva membuka ke atas
\(y = ax^2 + bx + c, \: a > 0\)
|
Domain
\(- \sim \: < x < \: \sim\)
Range \(\{y \geq y_{\text{min}}\}\)
Menentukan x puncak \(x_{\text{puncak}} = - \dfrac {b}{2a}\)
Menentukan y puncak Substitusi nilai \(x_{\text{puncak}}\) ke dalam persamaan fungsi untuk mendapatkan nilai y |
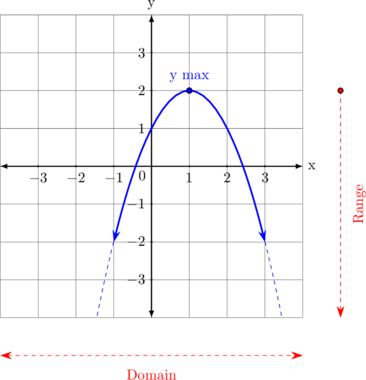
| Kurva membuka ke bawah
\(y = ax^2 + bx + c, \: a < 0\)
|
Domain
\(- \sim \: < x < \: \sim\)
Range \(\{y \leq y_{\text{max}}\}\) |
| C. Fungsi Akar | |
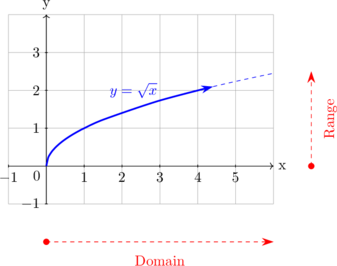
| \(y = \sqrt{x}\)
|
Domain
\(x \geq 0\)
Range \(y \geq 0\) |
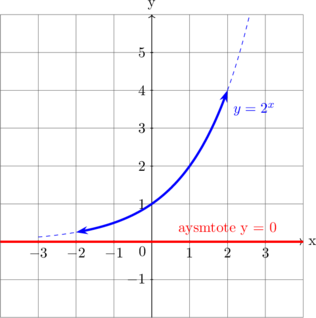
| D. Fungsi Eksponen | |
| \(y = a^x\)
|
Domain
\(\{x \in R\}\)
Range \(\{y > 0\}\)
Asymtote: \(y = 0\) |
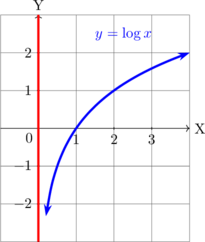
| E. Fungsi Logaritma | |
| \(y = \log x\)
|
Domain
\(x > 0\)
Range \(\{y \in R\}\)
Asymtote: \(x = 0\) |
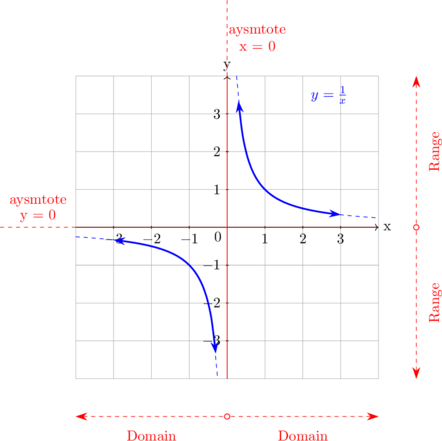
| F. Fungsi Pecahan | |
| \(y = \dfrac 1x\)
|
Asymtote datar
\(y = 0\)
Asymtote tegak \(x = 0\)
Domain \(\{x \neq 0\}\)
Range \(\{y \neq 0\}\) |
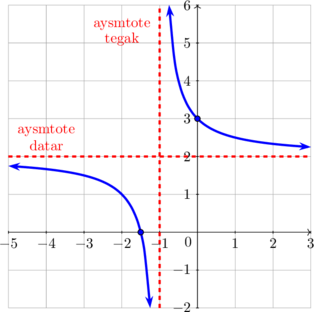
| G. Fungsi Pecahan | |
| \(y = \dfrac {ax + b}{cx + d}\)
|
Asymtote datar
\(y = \dfrac ac\)
Asymtote tegak \(cx + d = 0\) \(x = - \dfrac dc\)
Domain \(\{x \neq \text{ asymtote tegak}\}\)
Range \(\{y \neq \text{ asymtote datar}\}\) |
SOAL LATIHAN