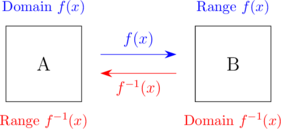
Fungsi \(f(x)\) memetakan \(A \rightarrow B\) dan fungsi \(f^{-1}(x)\) memetakan \(B \rightarrow A\)
Sebuah fungsi memiliki fungsi invers apabila fungsi tersebut merupakan fungsi korespondensi satu-satu, artinya, satu nilai X untuk satu nilai Y dan sebaliknya.
SIFAT-SIFAT FUNGSI INVERS
(1) \(D_f = R_{f^{-1}}\)
Domain dari \(f\) adalah range dari \(f^{-1}\)
(2) \(R_f = D_{f^{-1}}\)
Range dari \(f\) adalah domain dari \(f^{-1}\)
INVERS DARI KOMPOSISI FUNGSI
\((f \circ g)^{-1} (x) = (g^{-1} \circ f^{-1}) \: (x)\)
KOMPOSISI DARI FUNGSI DAN FUNGSI INVERS
\((f \circ f^{-1})(x) = (f^{-1} \circ f)(x) = x\)
SOAL LATIHAN