HCF and LCM
Prime Factorization
Determine the prime factorization by factor tree diagram:
Prime factorization of 100
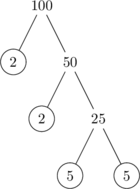
\(100 = 2^2 \times 5^2\)
Prime factorization of 120
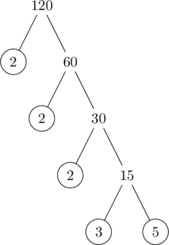
\(120 = 2^3 \times 3 \times 5\)
Highest Common Factor (HCF)
HCF of two or more numbers is the greatest number that can divide these numbers.
For example the HCF of 100 and 120 is 20, because 20 is the greatest number that can divide 100 and 120.
Determine the HCF of 100 and 120:
1. Find the prime factorization of 100 and 120
\(100 = 2^2 \times 5^2\)
\(120 = 2^3 \times 3 \times 5\)
2. Find the common factors with the smallest power and then multiply it
\(100 = {\color {red} 2^2} \times {\color {blue} 5^2}\)
\(120 = {\color {red} 2^3} \times 3 \times {\color {blue} 5}\)
HCF = \(2^2 \times 5 = 20\)
Lowest Common Multiply (LCM)
LCM of two or more numbers is the smallest number that is the common multiple of these numbers.
For example, the LCM of 100 and 120 is 600, because 600 is the smallest number that is the common multiple of 100 and 120.
Determine the LCM of 100 and 120:
1. Find the prime factorization of 100 and 120
\(100 = 2^2 \times 5^2\)
\(120 = 2^3 \times 3 \times 5\)
2. Multiply all the factors of the 100 and 120 (choose the greatest power)
\(100 = 2^2 \times {\color {red} 5^2}\)
\(120 = {\color {red} 2^3} \times {\color {red} 3} \times 5\)
LCM = \(2^3 \times 3 \times 5^2 = 600\)
Exercise

