Jika diketahui grafik suatu fungsi linear, kita dapat menentukan persamaan fungsinya.
Rumus-rumus yang digunakan
| No | Keterangan | Rumus |
| 1 | Menentukan gradien | \(m = \dfrac {y_2 - y_1}{x_2 - x_1}\)
\(m = \tan \alpha\) |
| 2 | Diketahui titik \((a,0)\) dan \((0,b)\) | \(\dfrac xa + \dfrac yb = 1\) |
| 3 | Diketahui gradien dan titik \((x_1,y_1)\) | \(y - y_1 = m \:.\: (x - x_1)\) |
| 4 | Diketahui dua titik \((x_1,y_1)\) dan \((x_2,y_2)\) | \(\dfrac {y - y_1}{y_2 - y_1} = \dfrac {x - x_1}{x_2 - x_1}\) |
| 5 | Dua garis sejajar | \(m_1 = m_2\) |
| 6 | Dua garis saling tegak lurus | \(m_1 \:.\: m_2 = -1\) |
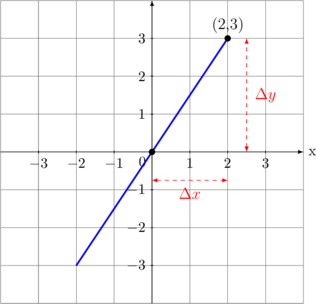
Contoh 01
Garis melalui titik \((0,0)\) → \(\bbox[5px, border: 2px solid red] {y = mx}\)
| No | Grafik | Persamaan |
| 1 |
|
Menentukan Gradien m
\(m = \dfrac {y_2 - y_1}{x_2 - x_1}\) \(m = \dfrac{3 - 0}{2 - 0}\) \(\bbox[5px, border: 2px solid magenta] {m = \dfrac{3}{2}}\)
Persamaan Fungsi \(y = \dfrac{3}{2} x\) |
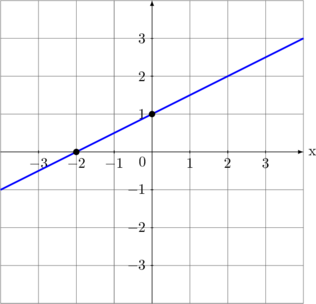
Contoh 02
Garis melalui titik \((a,0)\) dan \((0,b)\) → \(\bbox[5px, border: 2px solid red] {y = mx + c}\)
| No | Grafik | Persamaan |
| 1 |
|
\(\dfrac{x}{a} + \dfrac{y}{b} = 1\)
\(\dfrac{x}{-2} + \dfrac{y}{1} = 1\) \(x - 2y = -2\) |
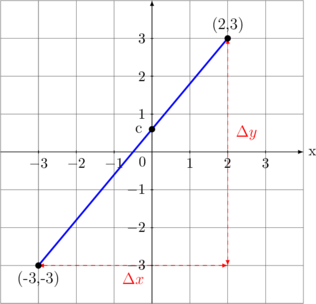
Contoh 03
Garis melalui titik sembarang → \(\bbox[5px, border: 2px solid red] {y = mx + c}\)
| No | Grafik | Persamaan |
| 1 |
|
Menentukan gradien m \(m = \dfrac {y_2 - y_1}{x_2 - x_1}\) \(m = \dfrac{3 - (-3)}{2 - (-3)}\) \(\bbox[5px, border: 2px solid magenta] {m = \dfrac{6}{5}}\)
Menentukan nilai c \((2,3) \rightarrow 3 = \dfrac{6}{5} (2) + c\) \(3 = \dfrac{12}{5} + c\) \(c = 3 - \dfrac{12}{5}\) \(\bbox[5px, border: 2px solid magenta] {c = \dfrac{3}{5}}\)
Persamaan garis \(y = \dfrac{6}{5} x + \dfrac{3}{5}\)
|
Contoh-contoh soal lainnya (variasi) dapat dilihat pada latihan soal.