Gaya Sentripetal
A. Percepatan sentripetal
Percepatan sentripetal adalah percepatan yang muncul pada benda yang bergerak melingkar.
Percepatan sentripetal selalu mengarah pada pusat lingkaran.
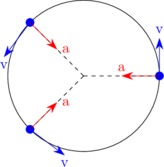
\(a_s = \dfrac {v^2}{R} = \omega^2 \:.\: R\)
B. Gaya sentripetal
Sama seperti percepatan sentripetal, gaya sentripetal juga bekerja pada benda yang bergerak melingkar dan arahnya menuju pusat lingkaran.
\(F_s = m \:.\: a_s\)
\(F_s = m \:.\: \dfrac {v^2}{R} = m \:.\: \omega^2 \:.\: R\)
C. Ayunan Konis
Sebuah batu diikat pada ujung tali dan diputar horizontal seperti gambar di bawah ini:

Diagram gaya
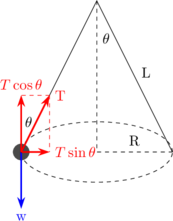
\begin{equation*} \begin{split} \Sigma F_x & = m \:.\: a_s \\\\ T \sin \theta & = m \:.\: \frac {v^2}{R} \quad {\color {red} \dotso \: (1)} \end{split} \end{equation*}
\begin{equation*} \begin{split} \Sigma F_y & = 0 \\\\ T \cos \theta & = m \:.\: g \quad {\color {red} \dotso \: (2)} \end{split} \end{equation*}
Eliminasi persamaan (1) dan (2)
\begin{equation*} \begin{split} \frac {\cancel{T} \sin \theta}{\cancel{T} \cos \theta} & = \frac {m \:.\: \dfrac {v^2}{R}}{m \:.\: g } \\\\ \tan \theta & = \frac {\dfrac {v^2}{R}}{g} \\\\ \tan \theta & = \frac {v^2}{g R} \\\\ v^2 & = gR \tan \theta \\\\ v & = \sqrt{gR \tan \theta} \end{split} \end{equation*}
\begin{equation*} \begin{split} \sin \theta & = \frac {R}{L} \\\\ R & = L \sin \theta \end{split} \end{equation*}
D. Tikungan jalan dengan kemiringan θ
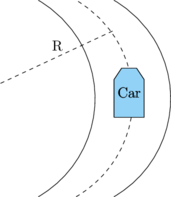
Diagram gaya
\begin{equation*} \begin{split} \Sigma F_x & = m \:.\: a_s \\\\ N \sin \theta & = m \:.\: \frac {v^2}{R} \quad {\color {red} \dotso \: (1)} \end{split} \end{equation*}
\begin{equation*} \begin{split} \Sigma F_y & = 0 \\\\ N \cos \theta & = m \:.\: g \quad {\color {red} \dotso \: (2)} \end{split} \end{equation*}
Eliminasi persamaan (1) dan (2)
\begin{equation*} \begin{split} \frac {\cancel{N} \sin \theta}{\cancel{N} \cos \theta} & = \frac {\cancel{m} \:.\: \dfrac {v^2}{R}}{\cancel{m} \:.\: g } \\\\ \tan \theta & = \frac {\dfrac {v^2}{R}}{g} \\\\ \tan \theta & = \frac {v^2}{g \:.\: R} \\\\ v^2 & = g \:.\: R \:.\: \tan \theta \\\\ v & = \sqrt{g \:.\: R \:.\: \tan \theta} \end{split} \end{equation*}
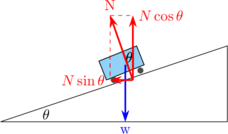
E. Tikungan jalan dengan koefisien gesekan μ

Diagram gaya
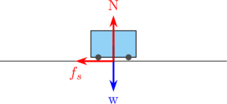
\begin{equation*} \begin{split} \Sigma F_x & = m \:.\: a_s \\\\ f_s & = m \:.\: a_s \\\\ \mu_s \:.\: N & = m \:.\: \frac {v^2}{R} \quad {\color {red} \dotso \: (1)} \end{split} \end{equation*}
\begin{equation*} \begin{split} \Sigma F_y & = 0 \\\\ N & = m \:.\: g \quad {\color {red} \dotso \: (2)} \end{split} \end{equation*}
Eliminasi persamaan (1) dan (2)
\begin{equation*} \begin{split} \frac {\mu_s \:.\: \cancel{N}}{\cancel{N}} & = \frac {\cancel{m} \:.\: \dfrac {v^2}{R}}{\cancel{m} \:.\: g } \\\\ \mu_s & = \frac {\dfrac {v^2}{R}}{g} \\\\ \mu_s & = \frac {v^2}{g \:.\: R} \\\\ v^2 & = g \:.\: R \:.\: \mu_s \\\\ v & = \sqrt{g \:.\: R \:.\: \mu_s} \end{split} \end{equation*}
SOAL LATIHAN

