Set
A set is a collection of well-defined objects
A set is well-defined if we are able to tell whether or not any particular object is an element of the set
Example:
Which of the following are well-defined sets?
(1) All the tall girls of the school
(2) All the letters in the word "mathematics"
(3) All the hardworking teachers in a school
(4) All the honest members in the family
Answer: (2)
All the letters in the word "mathematics" is well-defined sets
B = {m, a, t, h, e, i, c, s}
The following conventions are used with sets:
- Capital letters are used to denote sets
- Curly braces { } denote a list of elements in a set
- Lowercase letters are used to denote elements of sets
Example:
A is the set of vowels
A = {a, i, u, e, o}
The elements in the sets are depicted in either the statement form, set-builder notation form or roster form
1. Statement form
A = {prime numbers between 10 and 30}
2. Set-builder notation
A = {x| 10 < x < 30, x ∈ prime numbers}
We read it as, "A is the set of all x such that x is more than10 but less than 30 and x belongs to prime numbers"
3. Roster form
A = {11, 13, 17, 19, 23, 29}
Elements Of a Set
An element is a member of a set.
Notation:
∈ means “is an element of”
∉ means “is not element of”
Cardinality
The number of elements of a set is expressed as n(A)
Example:
A = {positive integers between −3 and 3}
A = {1, 2}
1 ∈ A {1 is an element of A}
2 ∈ A {2 is an element of A}
3 ∉ A {3 is not element of A}
n(A) = 2
Empty Set and Infinite Set
Null or empty set
Set with no elements
Example:
The sets of triangles having 4 sides
It is an empty set, because every triangle has 3 sides
Infinite set
The element cannot be listed (unlimited)
Example:
- Set of all point in a line segment
- Set of all natural numbers
- Set of all integers
Subset
\(\text{A}\) is a subset of \(\text{A}\) (\(\text{A}\subseteq \text{B}\)) if and only if every element of \(\text{A}\) is in \(\text{B}\).
The total number of subsets of a set with n elements is \(2^{n}\).
Example:
\(\text{P} = \lbrace 5, 10, 15, 20 \rbrace\)
\(\text{Q} = \lbrace 5, 10, 15, 20, 25, 30 \rbrace\)
\(\text{P}\) is a proper subset of \(\text{Q}\) because the element 25 and 30 is not in the set \(\text{P}\). (\(\text{P} \subset \text{Q}\))
The number of subset of \(\text{Q}\) is \(2^6 = 64\).
Example:
Find the number of subsets of \(\text{P} = \lbrace \text{a, b, c, d, e, f}\rbrace\) that contain exactly 3 elements
The total number of subsets of \(\text{P}\) is \(2^{6}\)
Using Pascal's triangle:

So, the number of subsets of \(\text{P}\) that contain exactly 3 elements is 20.
Equal Sets and Equivalent Sets
Two sets A and B are equal if they contain exactly the same elements
Example:
A = {1, 2, 4} and B = {4, 2, 1}
So set A is equal set B (A = B)
Two sets A and B are said to be equivalent if they have the same cardinality i.e. n(A) = n(B)
Example:
A = {a, i, u, e, o} and B = {2, 3, 5, 7, 11}
Set A is equivalent set B (A ∼ B) because n(A) = n(B) = 5
Universal Set
A universal set is the set of all elements or members of all related sets
Example :
Describe one possible universal set for each of the following sets!
1. {4, 6, 8, 10}
2. {Neptune, Saturn}
3. {cat, dog}
Solution:
1. U = the set of even numbers
2. U = the set of planets in our solar system
3. U = the set of pets
Disjoint Set and Joint Set
Disjoint set is two or more sets which have no elements in common
Example:
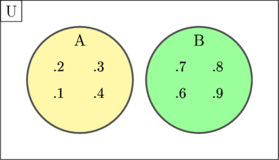
\(\text{U} = \lbrace 1, 2, 3, 4, 6, 7, 8, 9\rbrace\)
\(\text{A} = \lbrace 1, 2, 3, 4\rbrace\)
\(\text{B} = \lbrace 6, 7, 8, 9\rbrace\)
Set A and B are called disjoint set
Joint set is two or more sets which have elements in common
Example:
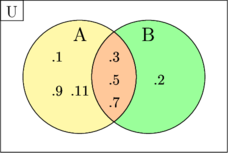
\(\text{U} = \lbrace 1, 2, 3, 5, 7, 9, 11 \rbrace\)
\(\text{A} = \lbrace 1, 3, 5, 7, 9, 11\rbrace\)
\(\text{B} = \lbrace 2, 3, 5, 7\rbrace\)
Set A and B is joint set because they have elements in common {3, 5, 7}
Exercise
