Himpunan
Himpunan adalah kumpulan benda atau objek yang dapat didefinisikan dengan jelas dan dianggap sebagai satu kesatuan.
Contoh:
Dari kumpulan berikut, manakah yang merupakan himpunan?
(1) Kumpulan siswa yang memiliki tubuh tinggi di sekolah X.
(2) Kumpulan siswa yang memiliki tinggi lebih dari 160 cm di sekolah X.
(3) Kumpulan artis K-POP tenar pada tahun 2020.
(4) Kumpulan artis K-POP yang memiliki 1 juta subscriber pada akun youtubenya.
Jawaban:
Yang merupakan himpunan adalah (2) dan (4) karena didefinisikan dengan jelas.
Menyatakan himpunan
1. Dengan kalimat
A = {bilangan prima antara 10 sampai 30}
2. Dengan notasi pembentuk himpunan
A = {x| 10 < x < 30, x ∈ bilangan prima}
3. Dengan mendaftar anggota himpunan
A = {11, 13, 17, 19, 23, 29}
Penulisan himpunan
1. Nama himpunan ditulis dengan huruf kapital (A, B, C, ...).
2. Anggota himpunan ditulis di dalam kurung kurawal {}.
3. Jika anggota himpunan berupa huruf maka ditulis dengan huruf kecil (a, b, c, ...).
Anggota dari himpunan
Anggota dari suatu himpunan disebut dengan elemen, dilambangkan dengan \(\in\), sebaliknya yang tidak tidak termasuk anggota himpunan dilambangkan dengan \(\notin\).
Banyaknya anggota himpunan dinyatakan dengan n( ).
Contoh:
X adalah himpunan huruf vokal, maka X = {a, i, u, e, o}
n(X) = 5
u \(\in\) X
p \(\notin\) X
Himpunan kosong dan Himpunan tak hingga
Himpunan kosong
Himpunan yang tidak memiliki anggota.
Contoh:
Himpunan segitiga yang memiliki 4 buah sisi.
Himpunan tak hingga
Himpunan yang jumlah anggotanya tidak terbatas.
Contoh:
Himpunan semua bilangan asli.
Himpunan bagian
\(\text{A}\) disebut himpunan bagian dari \(\text{B}\) (\(\text{A}\subset \text{B}\)) jika dan hanya jika setiap anggota dari \(\text{A}\) merupakan anggota dari \(\text{B}\).
Jumlah himpunan bagian dari sebuah himpunan dengan banyak anggota \(n\) adalah \(2^n\).
Contoh:
\(\text{P} = \lbrace 5, 10, 15, 20 \rbrace\)
\(\text{Q} = \lbrace 5, 10, 15, 20, 25, 30 \rbrace\)
\(\text{P}\) adalah himpunan bagian dari \(\text{Q}\) karena ada anggota dari \(\text{Q}\) yaitu 25 dan 30 tidak berada di \(\text{P}\). (\(\text{P} \subset \text{Q}\)).
Banyaknya himpunan bagian dari \(\text{Q}\) adalah \(2^6 = 64\).
Example:
Find the number of subsets of \(\text{P} = \lbrace \text{a, b, c, d, e, f}\rbrace\) that contain exactly 3 elements
The total number of subsets of \(\text{P}\) is \(2^{6}\)
Using Pascal's triangle:

So, the number of subsets of \(\text{P}\) that contain exactly 3 elements is 20.
Himpunan Sama dan Himpunan Ekuivalen
Dua himpunan A dan B dikatakan sama jika memiliki anggota-anggota yang sama
Contoh:
A = {1, 2, 4} and B = {4, 2, 1}
Karena himpunan A dan B memiliki anggota-anggota yang sama, maka himpunan A dan himpunan B adalah sama (A = B)
Dua himpunan A dan B dikatakan ekuivalen jika memiliki jumlah anggota yang sama n(A) = n(B)
Contoh:
A = {a, i, u, e, o} dan B = {2, 3, 5, 7, 11}
Himpunan A ekuivalen dengan B (A ∼ B) karena n(A) = n(B) = 5
Himpunan Semesta
Himpunan semesta adalah himpunan yang berisikan semua anggota atau objek yang sedang dibicarakan
Contoh :
Tentukan sebuah himpunan semesta yang mungkin dari setiap himpunan berikut!
- {4, 6, 8, 10}
- {Neptunus, Saturnus}
- {kucing, anjing}
Solusi:
- S = himpunan bilangan genap
- S = himpunan planet-planet dalam sistem tata surya kita
- S = himpunan binatang peliharaan
Himpunan Saling Lepas dan Tidak Saling Lepas
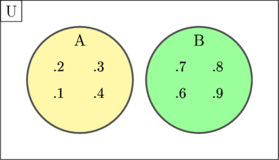
Himpunan saling lepas adalah 2 atau lebih himpunan yang anggota-anggotanya tidak ada yang sama
Contoh:
\(\text{S} = \lbrace 1, 2, 3, 4, 6, 7, 8, 9\rbrace\)
\(\text{A} = \lbrace 1, 2, 3, 4\rbrace\)
\(\text{B} = \lbrace 6, 7, 8, 9\rbrace\)
Himpunan A dan B saling lepas karena A dan B tidak memiliki anggota yang sama
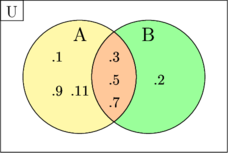
Himpunan tidak saling lepas adalah 2 atau lebih himpunan yang memiliki anggota yang sama
Contoh:
\(\text{U} = \lbrace 1, 2, 3, 5, 7, 9, 11 \rbrace\)
\(\text{A} = \lbrace 1, 3, 5, 7, 9, 11\rbrace\)
\(\text{B} = \lbrace 2, 3, 5, 7\rbrace\)
Himpunan A dan B tidak saling lepas karena memiliki anggota yang sama yaitu {3, 5, 7}
SOAL LATIHAN
