Garis Singgung

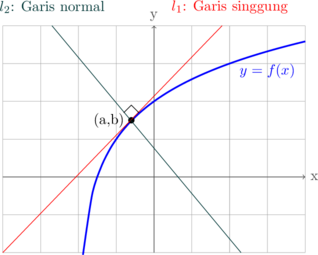
Persaman garis singgung pada kurva $y=f(x)$ di titik $(a,b)$ dapat ditentukan dengan:

(1) Menentukan gradien garis singgung

$m=y^{\prime }=f^{\prime }(a)$

(2) Menentukan persamaan garis singgung

$y-y_1=m.(x-x_1)$

Garis Normal

Garis normal adalah garis yang tegak lurus garis singgung pada titik yang sama.

Persaman garis normal pada kurva $y=f(x)$ di titik $(a,b)$ dapat ditentukan dengan:

(1) Menentukan gradien garis singgung

$m=y^{\prime }=f^{\prime }(a)$

(2) Menentukan gradien garis normal

$m_1.m_2=-1$

(2) Menentukan persamaan garis normal

$y-y_1=m.(x-x_1)$

Contoh 01

Tentukan persamaan garis singgung dan garis normal pada kurva $f(x)=x^3+4x^2-5x+1$ di titik $(1,2)$.

Garis singgung

Garis normal