Fungsi Naik dan Fungsi Turun
Interval fungsi naik dan fungsi turun dapat ditentukan dengan cara:
Fungsi naik → \(f' (x)>0\)
Fungsi turun → \(f' (x)<0\)
Contoh 01
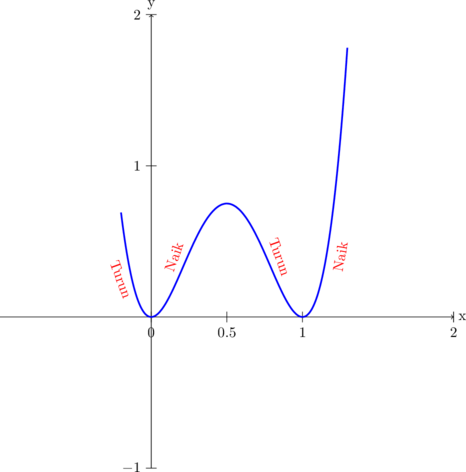
Tentukan naik turunnya kurva \(y=12 x^4 - 24x^3 + 12x^2\)
Turunan
\begin{equation*} \begin{split} & f' (x) = 0\\\\ & 48 x^{3} - 72 x^{2} + 24 x = 0 \\\\ & 24 x \:.\: (2x^{2} - 3x + 1) = 0\\\\ & 24x \:.\: (2x - 1)(x - 1) = 0\\\\ & x = 0 \text{ atau } x = \frac{1}{2} \text{ atau } x = 1 \end{split} \end{equation*}
Harga nol fungsi: 0, ½, 1
![]()
Kurva turun pada interval \(x < 0\) dan \(\frac 12 < x < 1\)
Kurva naik pada interval \(0 < x < \frac 12 \) dan \(x > 1\)
Uji titik untuk menentukan tanda + atau −
\(f'(x) = 24x \:.\: (2x - 1)\:.\: (x - 1) \)
\(f' (2) =24 \:.\: 2 \:.\: (2 \:.\: 2 - 1)\:.\: (2 - 1) > 0 \)
Pada \(x = 2\), fungsi bernilai positif.
Karena semua pembuat nol berpangkat ganjil, maka tanda berubah selang seling.
Titik Stationer
Titik stationer
\begin{equation*} f'(x) = 0 \end{equation*}
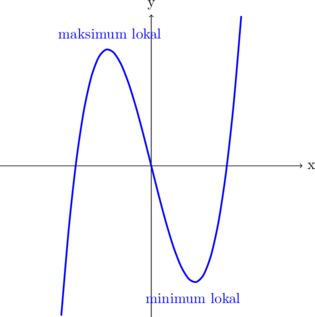
Jenis titik stationer
\begin{equation*} \begin{split} f''(x) & > 0 \quad \text{titik minimum lokal} \\\\ f''(x) & < 0 \quad \text{titik maksimum lokal} \\\\ f''(x) & = 0 \quad \text{titik belok} \end{split} \end{equation*}

Contoh Soal
Diketahui kurva \(f(x)=\dfrac{1}{5} x^{5}-\dfrac{1}{3} x^{3}\).
Tentukan titik-titik stasioner kurva dan jenisnya.
Koordinat titik stasioner
\begin{equation*} \begin{split} & f(x)=\frac{1}{5} x^{5}-\frac{1}{3} x^{3} \\\\ & f' (x) =0\\\\ & x^{4}-x^{2} =0\\\\ & x^{2} \:.\: (x^{2}-1) =0\\\\ & x^2 \:.\: (x+1) \:.\: (x-1) =0\\\\ & x=0 \text{ atau } x=-1 \text{ atau } x=1 \end{split} \end{equation*}
Titik x = −1
\begin{equation*} \begin{split} f(-1) & = \frac{1}{5} (-1)^{5}-\frac{1}{3} (-1)^{3} \\\\ f(-1) & = \frac{2}{15} \end{split} \end{equation*}
Koordinat titik \(\left(-1,\dfrac{2}{15} \right)\)
Titik x = 0
\begin{equation*} \begin{split} f(0) & = \frac{1}{5} (0)^{5}-\frac{1}{3} (0)^{3} \\\\ f(0) & = 0 \\\\ \end{split} \end{equation*}
Koordinat titik \((0,0)\)
Titik x = 1
\begin{equation*} \begin{split} f(1) & = \frac{1}{5} (1)^{5}-\frac{1}{3} (1)^{3} \\\\ f(1) & = -\frac{2}{15} \end{split} \end{equation*}
Koordinat titik \(\left(1,-\dfrac{2}{15} \right)\)
Menentukan jenis titik stasioner dengan uji turunan kedua:
\begin{equation*} \begin{split} f(x) & =\frac{1}{5} x^{5}-\frac{1}{3} x^{3} \\\\ f'(x) & = x^{4}-x^{2} \\\\ f''(x)&=4x^{3}-2x \end{split} \end{equation*}
Titik \(\left (-1,\dfrac{2}{15} \right)\)
\begin{equation*} \begin{split} f''(-1) & = 4(-1)^{3}-2(-1) \\\\ f''(-1) & =-2 \: {\color[RGB]{0,0,255} < 0 \quad \text{(maksimum)}} \end{split} \end{equation*}
Titik \((0,0)\)
\begin{equation*} \begin{split} f''(0)&=4(0)^{3}-2(0) \\\\ f''(0)& =0 \quad {\color[RGB]{0,0,255} \text{(titik belok)}} \end{split} \end{equation*}
Titik \(\left(1,-\dfrac{2}{15} \right)\)
\begin{equation*} \begin{split} f''(1) & =4(1)^{3}-2(1) \\\\ f''(1) & = 2 \: {\color[RGB]{0,0,255} > 0 \quad \text{(minimum)}} \end{split} \end{equation*}
Sketsa Kurva
Langkah-langkah menggambar grafik:
- Tentukan titik potong grafik dengan sumbu X dan sumbu Y
- Tentukan titik-titik stationer
- Tentukan jenis stationer
Contoh
Sketsa kurva \(y = \dfrac 13 x^3 - x^2 - 2x + \dfrac 83\)
SOAL LATIHAN
