Diskriminan

$D = b^{2} - 4 a c$

$D > 0$ , 2 akar real berbeda

$D = 0$ , 2 akar real yang sama (akar kembar)

$D < 0$ , tidak memiliki akar real (akar imaginer)

Contoh

Diketahui persamaan kuadrat $2 x^{2} - 5 x - 3 = 0$

A. Tentukan nilai diskriminan dari persamaan kuadrat di atas

B. Dari jawaban (A), tentukan jenis akarnya

A. Diskriminan

$\begin{aligned} D & = b^{2} - 4 a c \\ D & = (- 5)^{2} - 4 (2) (- 3) \\ D & = 49 \end{aligned}$

B. Jenis akar

Karena $D > 0$ , maka persamaan memiliki dua akar real yang berbeda.

Rendered by QuickLaTeX.com

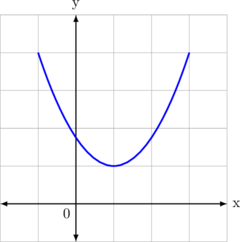
$a^{2} + b x + c > 0$

Syarat:

$a > 0$ dan $D < 0$

Karena kurva membuka ke atas, maka $a > 0$

Karena kurva tidak memotong sumbu X, maka $D < 0$

Rendered by QuickLaTeX.com

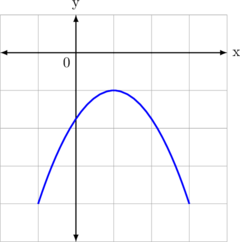
$a^{2} + b x + c < 0$

Syarat:

$a < 0$ dan $D < 0$

Karena kurva membuka ke bawah, maka $a < 0$

Karena kurva tidak memotong sumbu X, maka $D < 0$