Deret Aritmetika
Deret aritmetika adalah barisan atau deret dimana setiap dua suku berurutan memiliki selisih yang sama.
Bentuk umum barisan aritmetika adalah:
\(a, \: a + b, \: a + 2b, \: a + 3b, \: \dotso \)
Contoh:
\(1, 3, 5, 7, 9, \: \dotso\)
Setiap dua suku yang berdekatan memiliki selisih yang sama, yaitu 2.
\(a = 1, \: b = 2\)
Rumus
\(U_n = a + (n - 1)b\)
\(a\) : suku pertama
\(b\) : selisih suku dengan suku sebelumnya
\(n\) : banyaknya suku
\(U_n\) : suku ke-n
\(S_n = \dfrac{n}{2} \:.\: \left[a + U_n \right]\)
\(S_n = \dfrac{n}{2} \:.\: \left[2a + (n - 1)b \right] \)
\(S_n\) : jumlah suku-suku sampai dengan suku ke-n
Menentukan beda (b) pada barisan aritmetika
\(U_n - U_{n - 1} = b\)
Contoh:
\begin{equation*} \begin{split} U_2 - U_1 & = b \\\\ U_9 - U_6 & = 3b \end{split} \end{equation*}
Hubungan \(U_n\) dan \(S_n\)
\begin{equation*} U_n = S_n - S_{n - 1} \end{equation*}
Contoh:
\begin{equation*} \begin{split} U_5 & = S_5 - S_4 \\\\ U_9 & = S_9 - S_8 \end{split} \end{equation*}
Suku Tengah
\begin{equation*} U_T = \frac{1}{2} (a + U_n) \end{equation*}
\(U_T\) : suku tengah
Suku tengah hanya ada jika jumlah sukunya ganjil.
Bila jumlah sukunya genap, tidak memiliki suku tengah.
Sisipan
Jika di antara dua suku berturutan disisipkan sebanyak \(k\) bilangan sehingga membentuk barisan aritmetika baru, maka:
\begin{equation*} \begin{split} b' & = \frac{b}{k + 1} \\\\ n' & = n + (n - 1)k \end{split} \end{equation*}
\(b'\) : beda barisan yang baru setelah penyisipan
\(n'\) : jumlah suku yang baru setelah penyisipan
Deret Aritmetika Tingkat 2
Deret Aritmetika Tingkat 1
\(U_n = a + (n - 1) \:.\: b\)
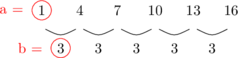
\(U_n = 1 + (n - 1) \:.\: 3\)
Deret Aritmetika Tingkat 2
\(U_n = a + (n - 1) \:.\: b + (n - 1)(n - 2) \:.\: \dfrac {c}{2!}\)

\(U_n = 5 + (n - 1) \:.\: 3 + (n - 1)(n - 2) \:.\: \dfrac {2}{2!}\)
SOAL LATIHAN

