Soal 4
Grafik fungsi \(y = k \: a^x + c\) seperti gambar di bawah ini.
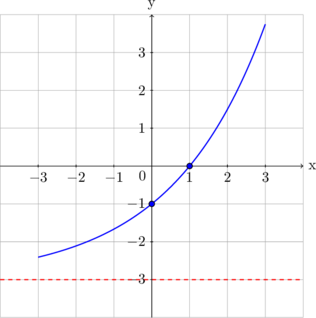
Nilai dari \(ka + c = \dotso\)
(A) \(-2\)
(B) \(-1\)
(C) \(0\)
(D) \(1\)
(E) \(2\)
Soal 5
Grafik fungsi \(y = 5^{x - 1} + 2\) mengalami transformasi pergeseran 2 unit ke arah kiri dan 1 unit ke arah bawah. Fungsi tersebut menjadi ...
(A) \(y = \frac{1}{125} \:.\: 5^{x} + 3\)
(B) \(y = \frac{1}{125} \:.\: 5^{x} + 1\)
(C) \(y = 5 \:.\: 5^{x} + 3\)
(D) \(y = 5 \:.\: 5^{x} + 1\)
(E) \(y = 7^{x - 1} + 2\)
Soal 7
Grafik fungsi \(y = k \:\: 5^{x} + c\) melalui titik \((1,28)\) dan \((-1,4)\). Nilai dari \(k - 2c = \dotso\)
(A) \(-2\)
(B) \(-1\)
(C) \(0\)
(D) \(1\)
(E) \(2\)
[/dt_sc_tab]
4. Latihan 1
LATIHAN 1
Soal 1
Diketahui:
-
- Nilai yang memenuhi persamaan \(\sqrt [3] {3^{x + 6}} = \dfrac{1}{\sqrt{27^{1 - x}}}\) adalah m
- Nilai yang memenuhi persamaan \(3^{2x - 1} \:.\: 27^{ \: x + 2} = 1\) adalah n
Nilai dari m + 2n = ...
(A) −2
(B) −1
(C) 0
(D) 1
(E) 2
Jawab: D
Persamaan pertama:
\begin{equation*}
\begin{split}
\sqrt [3] {3^{x + 6}} & = \frac{1}{\sqrt{27^{1 - x}}} \\\\
(3)^{\dfrac{x + 6}{3}} & = (3)^{\dfrac{-3(1 - x)}{2}} \\\\
\frac{x + 6}{3} & = \frac{-3(1 - x)}{2} \\\\
2(x + 6) & = -9((1 - x) \\\\
2x + 12 & = -9 + 9x \\\\
-7x & = -21 \\\\
x & = 3 \\\\
\end{split}
\end{equation*}
Persamaan kedua:
\begin{equation*}
\begin{split}
3^{2x - 1} \:.\: 27^{ \: x + 2} & = 1 \\\\
3^{2x - 1} \:.\: 3^{ \: 3x + 6} & = 3^0 \\\\
3^{2x - 1 + 3x + 6} & = 3^0 \\\\
5x + 5 & = 0 \\\\
5x & = -5 \\\\
x & = -1 \\\\
\end{split}
\end{equation*}
Nilai dari \(m + 2n = 3 + 2(-1) = 1\)
Soal 2
Nilai yang memenuhi persamaan \(2^{2x^2 - 5x + 1} = 5^{x^2 - 5x + 1}\) adalah \(x_1\) dan \(x_2\). Nilai dari \(x_1 + x_2 + x_1 \:.\: x_2 = \dotso\)
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Jawab: C
Satu-satunya kemungkinan jawaban adalah \(2x^2 - 5x + 1 = 0\) karena \(2^0 = 5^0 = 1\)
\(2x^2 - 5x + 1 = 0\)
\(a = 2, \: b = -5, \: c = 1\)
\(x_1 + x_2 = -\frac{b}{a} = -\frac{-5}{2}= \frac{5}{2}\)
\(x_1 \:.\: x_2 = \frac{c}{a} = \frac{1}{2}\)
\(x_1 + x_2 + x_1 \:.\: x_2 = \frac{5}{2} + \frac{1}{2} = 3\)
Soal 3
Nilai yang memenuhi persamaan \(2^{x} = 3^{1 - x}\) adalah ...
(A) \(\log_2 3\)
(B) \(\log_2 5\)
(C) \(\log_3 2\)
(D) \(\log_3 5\)
(E) \(\log_6 3\)
Jawab: E
\begin{equation*}
\begin{split}
2^{x} & = 3^{1 - x} \\\\
\log 2^{x} & = \log 3^{1 - x} \quad{\color{blue}\text{tambahkan log pada kedua ruas}}\\\\
x \log 2 & = (1 - x) \log 3\\\\
x \log 2 & = \log 2 - x \log 3\\\\
x \log 2 + x \log 3 & = \log 2 \\\\
x (\log 2 + \log 3) & = \log 2 \\\\
x \log 6 & = \log 2 \\\\
x & = \frac{\log 2}{\log 6}\\\\
x & = \log_6 2
\end{split}
\end{equation*}
Soal 4
Nilai x yang memenuhi persamaan \(5^{x + 1} + 5^{2 - x} = 30\) adalah \(x_1\) dan \(x_2\) dimana \(x_1 > x_2\). Maka \(x_1 - x_2 = \dotso\)
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Jawab: A
\begin{equation*}
\begin{split}
5^{x + 1} + 5^{2 - x} & = 30 \\\\
5^x \:.\: 5^1 + \frac{5^2}{5^ x} & = 30 \quad{\color{blue} \text{misalkan }m = 5^x}\\\\
5m + \frac{25}{m} & = 30 \quad{\color{blue}\text{kali m pada kedua ruas}}\\\\
5m^2 +25 & = 30m\\\\
m^2 + 5 & = 6m \\\\
m^2 - 6m + 5 & = 0 \\\\
(m - 5)(m - 1) & = 0 \\\\
m = 5 \text{ atau } & m = 1\\\\
5^x = 5 \text{ atau } & 5^x = 5^0 \quad{\color{blue}\text{ubah 1 menjadi }5^0}\\\\
x = 1 \text{ atau } & x = 0\\\\
\end{split}
\end{equation*}
Maka \(x_1 - x_2 = 1 - 0 = 1\)
Soal 5
Jumlah dari seluruh nilai x yang memenuhi persamaan \((x - 1)^{x^2 + 5x + 6} = (2x + 6)^{x^2 + 5x + 6}\) adalah ...
(A) −15
(B) −12
(C) −10
(D) −6
(E) −1
Jawab: C
Bentuk \((x - 1)^{x^2 + 5x + 6} = (2x + 6)^{x^2 + 5x + 6}\) memiliki dua solusi:
Solusi pertama
\begin{equation*}
\begin{split}
x - 1 & = 2x + 6 \\\\
-x & = 7 \\\\
x & = -7 \\\\
\end{split}
\end{equation*}
Solusi kedua
\begin{equation*}
\begin{split}
x^2 + 5x + 6 & =0 \\\\
(x + 3)(x + 2) & = 0 \\\\
x = -3 \text{ atau } & x = -2\\\\
\end{split}
\end{equation*}
Hasil dari solusi kedua harus diuji dimana \(x - 1)\) dan \(2x + 6\) tidak boleh sama dengan nol untuk nilai x yang didapat dari solusi kedua.
Untuk x = −3
\(x - 1 = -3 - 1 = -4\)
\(2x + 6 = 2(-3) + 6 = 0\) → karena sama dengan nol, maka x = −3 tidak dapat digunakan sebagai jawaban.
Untuk x = −2
\(x - 1 = -2 - 1 = -3\)
\(2x + 6 = 2(-2) + 6 = 2\)
HP = \(\{-7,-3\}\)
Soal 6
Banyaknya himpunan penyelesaian dari persamaan \((x + 1)^{2x - 4} = (x + 1)^{x^2 + 3x - 10}\) adalah ...
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Jawab: D
Bentuk \((x + 1)^{2x - 4} = (x + 1)^{x^2 + 3x - 10}\) memiliki empat solusi:
Solusi pertama
\begin{equation*}
\begin{split}
2x - 4 & = x^2 + 3x - 10 \\\\
x^2 + x - 6 & = 0 \\\\
(x + 3)(x - 2) & = 0 \\\\
x = -3 \text{ atau } & x = 2\\\\
\end{split}
\end{equation*}
Solusi kedua
\begin{equation*}
\begin{split}
x + 1 & = 1 \\\\
x & = 0 \\\\
\end{split}
\end{equation*}
Solusi ketiga
\begin{equation*}
\begin{split}
x + 1 & = 0 \\\\
x & = -1 \\\\
\end{split}
\end{equation*}
Solusi ketiga harus diuji dimana \(2x - 4\) dan \(x^2 + 3x - 10\) tidak boleh bernilai negatif untuk nilai x yang didapat dari solusi ketiga.
\(2x - 4 = 2(-1) - 4 = -6\) → karena bernilai negatif, maka x = −1 tidak dapat digunakan sebagai jawaban.
Solusi keempat
\begin{equation*}
\begin{split}
x + 1 & = -1 \\\\
x & = -2 \\\\
\end{split}
\end{equation*}
Solusi keempat harus diuji dimana \(2x - 4\) dan \(x^2 + 3x - 10\) keduanya harus bilangan genap atau keduanya bilangan untuk nilai x yang didapat dari solusi keempat.
\(2(-2) - 4 = 2(-2) - 4 = -8\)
\(x^2 + 3x - 10 = (-2)^2 + 3(-2) - 10 = -12\)
Karena keduanya bilangan genap, maka x = −2 dapat digunakan sebagai jawaban.
HP = \(\{-3,-2,0,2\}\)
Soal 7
Himpunan penyelesaian dari persamaan \(2^{x - 3} > -2\) adalah ...
(A) \(\{x < 2, \: x \: \varepsilon \: R\}\)
(B) \(\{x < 4, \: x \: \varepsilon \: R\}\)
(C) \(\{x > 4, \: x \: \varepsilon \: R\}\)
(D) \(\{ \: \}\)
(E) \(\{x \: \varepsilon \: R\}\)
Jawab: E
Bentuk eksponen \(a^x\) selalu menghasilkan nilai positif, maka untuk \(2^{x - 3} > -2\) semua bilangan real memenuhi.
Soal 8
Himpunan penyelesaian dari persamaan \(3^{x + 1} < -9\) adalah ...
(A) \(\{x < -10, \: x \: \varepsilon \: R\}\)
(B) \(\{x < -8, \: x \: \varepsilon \: R\}\)
(C) \(\{x > 10, \: x \: \varepsilon \: R\}\)
(D) \(\{ \: \}\)
(E) \(\{x \: \varepsilon \: R\}\)
Jawab: D
Bentuk eksponen \(a^x\) selalu menghasilkan nilai positif, maka untuk \(3^{x + 1} < -9\) tidak ada bilangan real yang memenuhi.
Soal 9
Himpunan penyelesaian dari persamaan \((64)^{x^2 - \frac{3}{4}x} \leq (\sqrt{8})^{x^2}\) adalah ...
(A) \(\{x \leq -1, x\geq 0, \: x \: \varepsilon \: R\}\)
(B) \(\{x \leq 0, x\geq 1, \: x \: \varepsilon \: R\}\)
(C) \(\{-1 \leq x \leq 0, \: x \: \varepsilon \: R\}\)
(D) \(\{0 \leq x \leq 1, \: x \: \varepsilon \: R\}\)
(E) \(\{x \: \varepsilon \: R\}\)
Jawab: D
\begin{equation*}
\begin{split}
(64)^{x^2 - \frac{3}{4}x} & \leq (\sqrt{8})^{x^2} \\\\
(8)^{2x^2 - \frac{3}{2}x} & \leq (8)^{\frac{1}{2} x^2} \\\\
2x^2 - \frac{3}{2}x & \leq \frac{1}{2} x^2 \\\\
\frac{3}{2} x^2 - \frac{3}{2}x & \leq 0 \\\\
\frac{3}{2} x ( x - 1) & \leq 0 \\\\
\end{split}
\end{equation*}
HNF = 0, 1

HP = \(\{0 \leq x \leq 1, \: x \: \varepsilon \: R\}\)
Soal 10
Himpunan penyelesaian dari persamaan \((0,2)^{x^2 - 3x} \leq (0,04)^{x + 3}\) adalah ...
(A) \(\{x \leq -2, x\geq 3, \: x \: \varepsilon \: R\}\)
(B) \(\{x \leq -3, x\geq 2, \: x \: \varepsilon \: R\}\)
(C) \(\{-2 \leq x \leq 3, \: x \: \varepsilon \: R\}\)
(D) \(\{-3 \leq x \leq 2, \: x \: \varepsilon \: R\}\)
(E) \(\{x \: \varepsilon \: R\}\)
Jawab: A
\begin{equation*}
\begin{split}
(0,2)^{x^2 - 3x} & \leq (0,04)^{x + 3} \\\\
(\frac{1}{5})^{x^2 - 3x} & \leq (\frac{1}{25})^{x + 3} \\\\
(\frac{1}{5})^{x^2 - 3x} & \leq (\frac{1}{5})^{2x + 6} \\\\
x^2 - 3x & \geq 2x + 6 \quad {\color{blue} \text{tanda berubah}} \\\\
x^2 - 5x - 6 & \geq 0 \\\\
(x - 3)(x + 2) & \geq 0 \\\\
\end{split}
\end{equation*}
HNF = −2, 3

HP = \(\{x \leq -2, x\geq 3, \: x \: \varepsilon \: R\}\)
Soal 11
Banyaknya bilangan bulat yang memenuhi dari persamaan \(2 \:.\: 4^x - 9 \:.\: 2^x + 4 < 0\) adalah ...
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Jawab: B
\begin{equation*}
\begin{split}
2 \:.\: 4^x - 9 \:.\: 2^x + 4 & < 0 \\\\
2 \:.\: 2^{2x} - 9 \:.\: 2^x + 4 & < 0 \quad {\color{blue} m = 2^x}\\\\
2m^2 - 9m + 4 & < 0 \\\\
(2m - 1)(m - 4) & < 0 \\\\
\end{split}
\end{equation*}
HNF = ½, 4

\(\frac{1}{2} < m < 4\)
\(\frac{1}{2} < m < 4\)
\(2^{-1} < 2^x < 2^2\)
\(-1 < x < 2\)
Bilangan bulat yang memenuhi adalah 0 dan 1
Soal 12
Jika \(f(x) = 3^x\), maka \(f(p + q) = ... \)
(A) \(f(p) + f(q)\)
(B) \(f(p) \:.\: f(q)\)
(C) \(\dfrac{f(p)}{f(q)}\)
(D) \([f(p)]^q\)
(E) \([f(q)]^p\)
Jawab: B
\begin{equation*}
\begin{split}
f(p + q) & = 3^{p + q} \\\\
& = 3^p \:.\: 3^q \\\\
& = f(p) \:.\: f(q) \\\\
\end{split}
\end{equation*}
Soal 13
Dalam sebuah eksperimen, bakteri berkembang biak menurut persamaan \(N = N_o \:.\: 2^{kt}\), dimana No dan k adalah suatu konstanta tertentu, N adalah jumlah bakteri setelah waktu tertentu dan t adalah waktu dalam menit. Mula-mula terdapat 10 bakteri dan dalam waktu 2 menit jumlah bakteri menjadi 20. Berapa waktu yang diperlukan untuk mencapai 10.000 bakteri?
(A) 6
(B) 12
(C) 15
(D) 18
(E) 20
Jawab: E
Mula-mula terdapat 10 bakteri → t = 0, N = 10
\begin{equation*}
\begin{split}
N & = N_o \:.\: 2^{kt} \\\\
10 & = N_o \:.\: 2^{0} \\\\
N_o & = 10 \\\\
\end{split}
\end{equation*}
Saat t = 2, N = 20
\begin{equation*}
\begin{split}
N & = 10 \:.\: 2^{kt} \\\\
20 & = 10 \:.\: 2^{2k} \\\\
2 & = 2^{2k} \\\\
1 & = 2k \\\\
k & = \tfrac{1}{2}
\end{split}
\end{equation*}
Persamaan menjadi \(N = 10 \:.\: 2^{\frac{1}{2}t}\)
Waktu yang dibutuhkan untuk mencapai 10.000 bakteri:
\begin{equation*}
\begin{split}
N & = 10 \:.\: 2^{\frac{1}{2}t} \\\\
10.000 & = 10 \:.\: 2^{\frac{1}{2}t} \\\\
1.000 & = 2^{\frac{1}{2}t} \quad {\color {blue} \text{tambahkan ln pada kedua ruas}}\\\\
\ln 1.000 & = \frac{1}{2}\:.\: t \ln 2 \\\\
t & = 19,9 \approx 20 \quad {\color {blue} \text{bulatkan ke atas}}\\\\
\end{split}
\end{equation*}
Soal 14
Grafik fungsi \(y = 2^{2x - 4} - 1\) ditunjukkan oleh ...
A
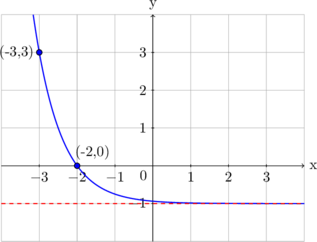
B
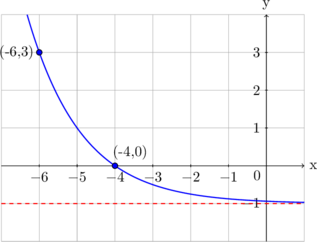
C
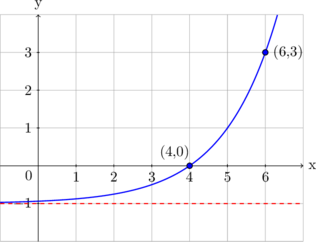
D
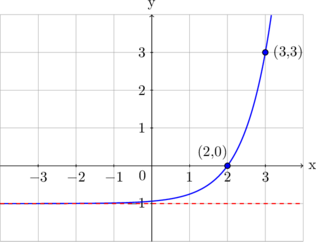
Jawab: D
fungsi \(y = 2^{2x - 4} - 1\) memiliki asymtot \(y = -1\)
Substitusi kedua titik yang diketahui pada gambar pada fungsi, maka yang memenuhi adalah gambar E
Soal 15
Grafik fungsi di bawah ini adalah ...
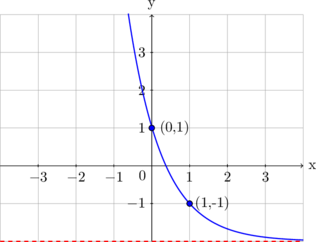
(A) \(y = (\frac{1}{3})^{x - 1} - 2\)
(B) \(y = (\frac{1}{3})^{x - 1} + 2\)
(C) \(y = (\frac{1}{3})^{x + 1} - 2\)
(D) \(y = (\frac{1}{3})^{x + 1} + 2\)
(E) \(y = (\frac{1}{3})^{x - 1}\)
Jawab: A
Grafik memiliki asymtot \(y = -2\) maka fungsi memiliki bentuk \(y = a^{x + b} - 2\)
Substitusi kedua titik yang diketahui pada gambar pada pilihan A dan C untuk mengetahui jawaban yang tepat (cara coba-coba).









